Lab10 - Localization with Bayes Filter

Objective

This lab is to implement grid localization using Bayes filter.

Keywords

Localization, Bayes Filter

Lab Tasks

Here, we simulate our robot on the grid. The robot state consists of three parts - $(x, y, \theta)$, and the robot’s world isa continuous space. (with the spans: $x \in [-1.6764, +1.9812)\text{meters}$, $y \in [-1.3716, +1.3716) \text{meter}$, $\theta \in [-180, +180) \text{degrees}$)

The grid cells are identical in size. The size of each grid cell (i.e resolution of the grid) along the $x$, $y$ and $\theta$ axes are 0.3048 m, 0.3048 meters and 20 degrees, respectively. The total number of cells along each axis are (12,9,18).

Task 1 - Compute Control

In this compute_control function, we compute the motion between the two adjacent points, based on the odometry motion model.

Function implementation:

Task 2 - Odometry Motion Model

From compute_control() function, we calculate the robot’s actual movement. Here, we use Gaussian distribution to calculate the probability of this movement.

Function implementation:

Task 3 - Prediction Step

Given the previous position and control vector, we use the model to get the probability matrix of current potential positions. We use the belief matrix to indicate the probabilities of positions. Here, if bel is smaller than 0.0001, it will tell that the probability is regarded as 0.

Function implementation:

Task 4 - Sensor Model

Here, we use the Gaussian model to calculate the probability of each sensor’s measurement.

Task 5 - Update Step

Here, we get the belief of the robot appearing on each grid using the multiplication of the measurement probability and the prediction belief. At last, to prevent the resulting value suffering from the floating point underflow when we multiply the probabilities, we normalize the belief.

The robot can find the position with the highest probability.

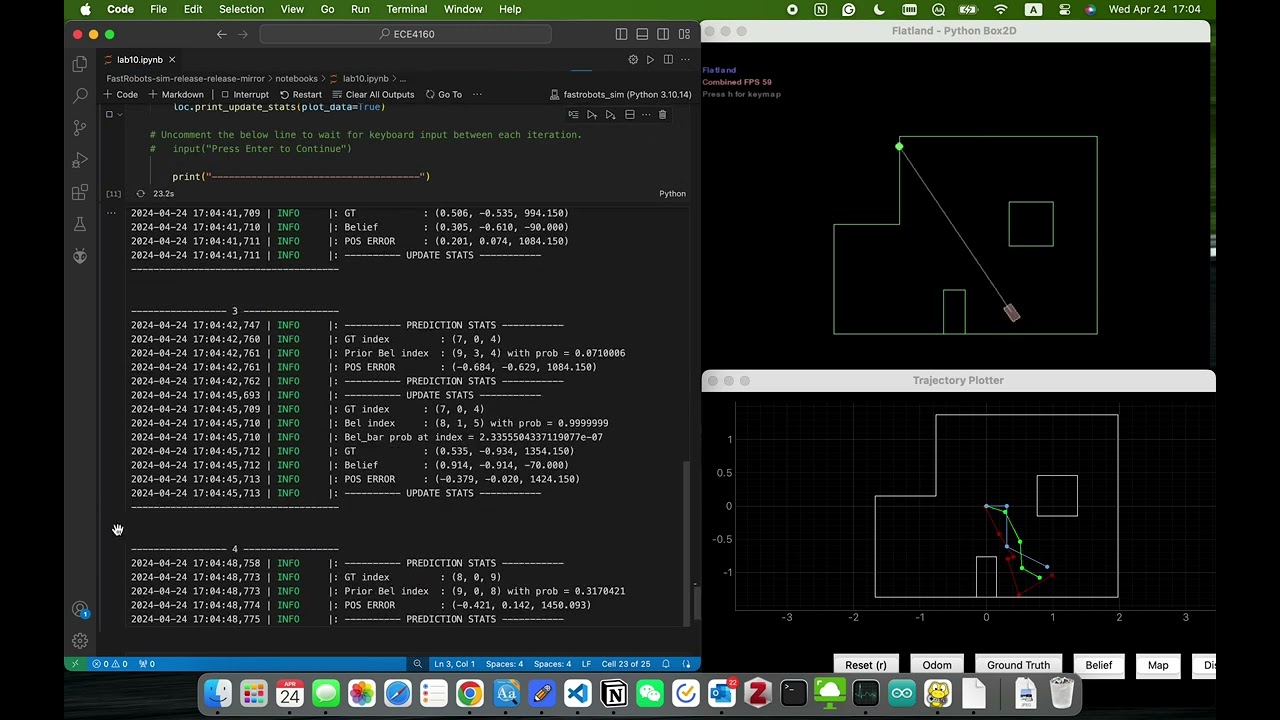
Simulation Demo

With the above implemented model, we can get the simulation shown as follows.

(Green path $\rightarrow$ Ground Truth, Blue path $\rightarrow$ the Belief of the Robot using Bayes Filter, Red path $\rightarrow$ Odometry Measurements)

where we can see that our model can greatly predict the positions of the robot.

Reference

Code mostly mirrored from Ignacio Romo.